为什么要引入浮点表示 @
-
编程困难,程序员要调节小数点的位置
-
数的表示范围小,为了能表示两个大小相差很大的数据,需要很长的机器字长。
- 例如:太阳的质量为 $0.2*10^{34}$ 克,一个电子的质量大约为 $0.9*10^{-27}$ 克,两者差距为 $10^{61}$ 以上,若用定点数据表示:$2^x > 10^{61}$,解得 $x>203$ 位。
-
数据存储单元的利用率往往很低。
浮点表示 @

浮点数的表示形式 @
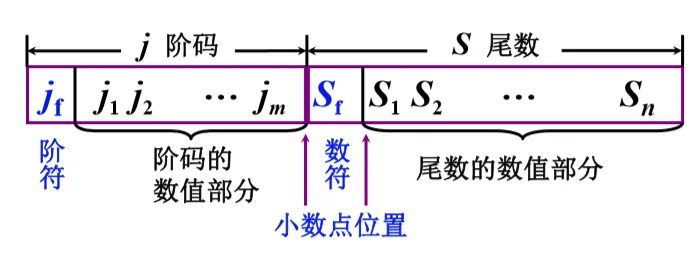
- Sf 代表浮点数的符号
- n 其位数反映浮点数的精度
- m 其位数反映浮点数的表示范围
- jf 和 m 共同表示小数点的实际位置
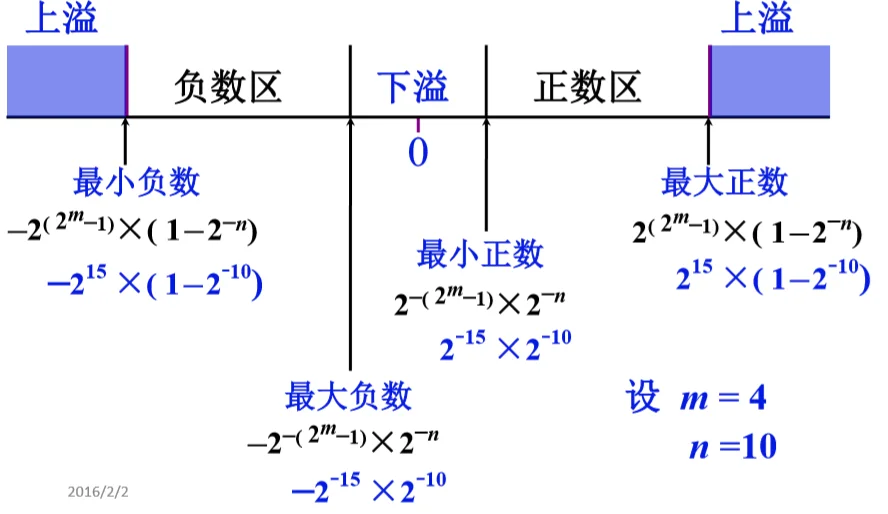
浮点数的表示范围 @
上溢: 阶码 > 最大阶码
下溢: 阶码 < 最小解码,按机器零处理
练习 @
设机器数字长为 24 位,欲表示 ±3 万的十进制数,试问在保证数的最大精度的前提下,除阶符、数符各取 1 位以外,阶码、尾数各取几位?

浮点数的规格化形式 @
- r=2,尾数最高位为 1
- r=4,尾数最高 2 位不全为 0
- r=8,尾数最高 3 位不全为 0
基数不同,浮点数的规格化形式不同。
浮点数的规格化 @
-
r=2
- 左规,尾数左移一位,阶码减 1
- 右规,尾数右移一位,阶码加 1
-
r=4
- 左规,尾数左移两位,阶码减 1
- 右规,尾数右移两位,阶码加 1
-
r=8
- 左规,尾数左移三位,阶码减 1
- 右规,尾数右移三位,阶码加 1
基础 r 越大,可表示的浮点数的范围越大基数 r 越大,浮点数的精度降低
例题 @
设 m=4,n=10,r=2,尾数规格化后的浮点数表示范围
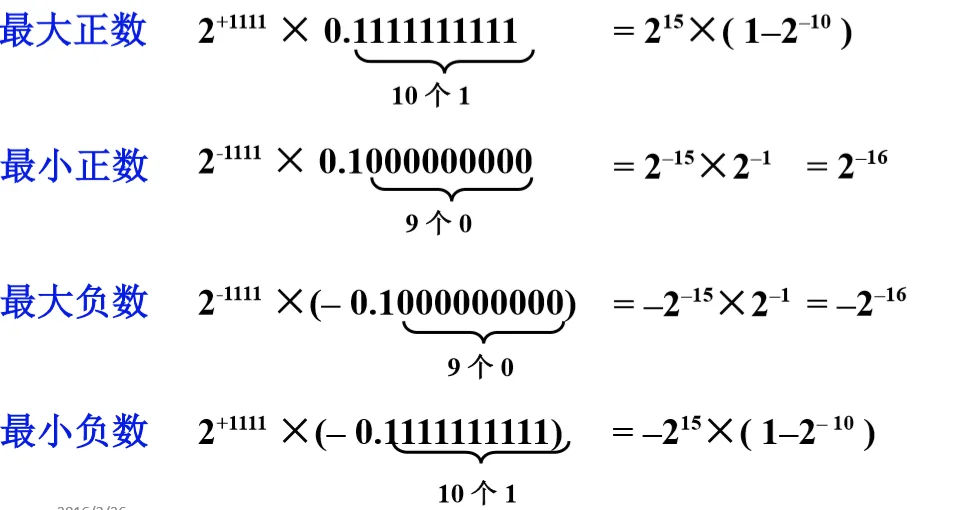
将 +19/128 写成二进制定点数、浮点数及在定点机和浮点机中的机器数形式。其中数值部分均取 10 位,数符取 1 位,浮点数阶码取 5 位(含一位阶符),尾数规格化。

19/128 用二进制表示形式,19 每次除 2,小数点向左移动一位。
将-58 表示成二进制定点数和浮点数,并写出它在定点机和浮点机中的三种机器数及阶码为移码、尾数为补码的形式。

机器零 @
- 当浮点数尾数为 0 时,不论其阶码为何值按机器零处理。
- 当浮点数阶码等于或小于它所表示的最小数时,不论尾数为何值,按机器零处理,如 m=4,n=10。
- 当阶码和尾数都用补码表示时,机器零为 x,xxxx;0.00…0, 阶码=-16: 1,0000;x.xx…x.
- 当阶码用移码,尾数用补码表示时,机器零为 0,0000;0.00…0,有利于机器中”判 0”电路的实现。
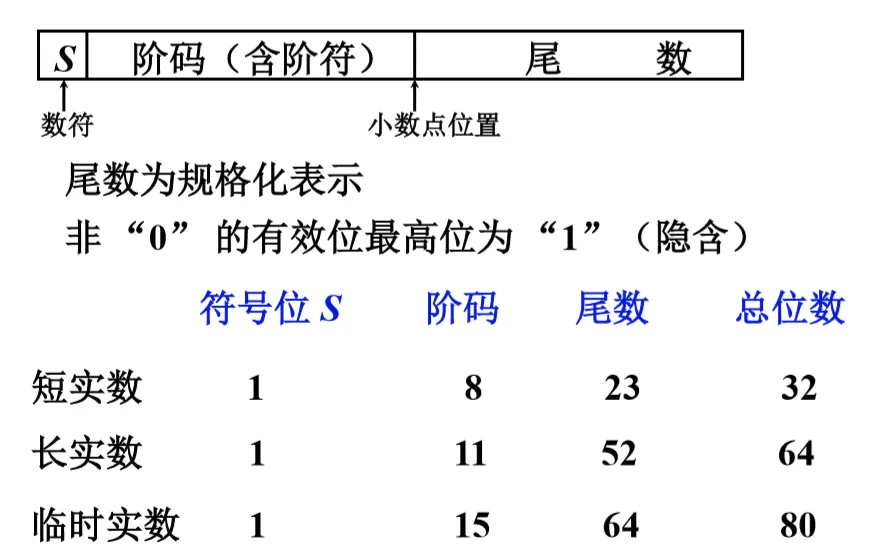
IEEE754 标准 @