浮点加减运算 @
$$ x = S_x \times 2^t, \quad y = S_y \times 2^t $$对阶 @
- 求阶差
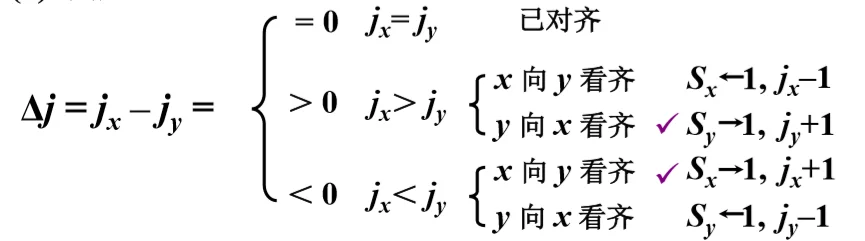
-
对阶就是判断两个浮点数的值是否相同,如果两数的阶码相同,直接可以加数值部分,即可完成相加,如果阶码不同,则需要对其进行对阶。
-
对阶原则,小阶向大阶看齐
如果大阶向小阶看齐,需要对其进行左移,容易将高位的 1 丢失,引发错误。而小阶向大阶看齐,需要对其进行右移,只会影响数据的精度,不会影响具体的数据大小
例如:$x=0.1101×2^{01},y=(−0.1010)×2^{11}$,求$x+y$
- 对阶
i. 求阶差:$[\Delta I]_{i\frac{1}{2}} = [I_s]_{i\frac{1}{2}}^k - [I_s]_{i\frac{1}{2}}^{k-1} = 00.01 - 11.10 = -2$,$f_x + 2$
ii. 对阶后 $[x]_{i\frac{1}{2}} = 00.11;00.0011$
- 尾数求和:$[S_x]_{i\frac{1}{2}} + [S_y]_{i\frac{1}{2}} = 00.0011 + 11.0110 = 11.1001$
所以 $[x+y]_{i\frac{1}{2}} = 00.11;11.1001$,$-[y_s]_{i\frac{1}{2}} \text{ 实际上等于 } [-f_s]_{i\frac{1}{2}}$
规格化 @
- 规格化数的定义,$r=2, \quad \frac{1}{2} \leq |S| < 1$
- 规格化数的判断

原码: 不论正数、负数,第一数位为 1 补码: 符号位和第一数位不同
特例:
-
$[-1/2]_{补}$ 不是规格化的数
$S = -1/2 = -0.100...0$
$[S]_{原} = 1.100...0$
$[S]_{补} = 1.100...0$
-
$[-1]_{补}$ 是规格化的数
$S = -1$
$[S]_{补} = 1.000...0$
左规 @
尾数左移一位,阶码-1,直到数符和第一数位不同为止
例:$[x+y]_{补} = 00,11;11.1001$
左规后$[x+y]_{补} = 00,10;11.0010$
则 $x+y=(-0.1110)\times2^{10}$
右规 @
当尾数溢出(>1)时,需要右规
即尾数出现 01.XX 或 10.XX 时,尾数右移一位,阶码 +1
例:$x = 0.1101 \times 2^{10}, y = 0.1011 \times 2^{01}$,求$x+y$
除阶符、数符外,阶码取 3 位,尾数取 6 位


舍入 @
在对阶和右规过程中,可能出现尾数末位丢失,引起误差,需考虑舍入。
- 0 舍 1 入法,如果末位是 0 丢弃,如果是 1 进位
- 恒置”1”法,末位始终置为 1
例如: $x=(−5/8)×2^{−5},y=(7/8)×2^{−4}$
除阶符、数符外,阶码取 3 位,尾数取 6 位。


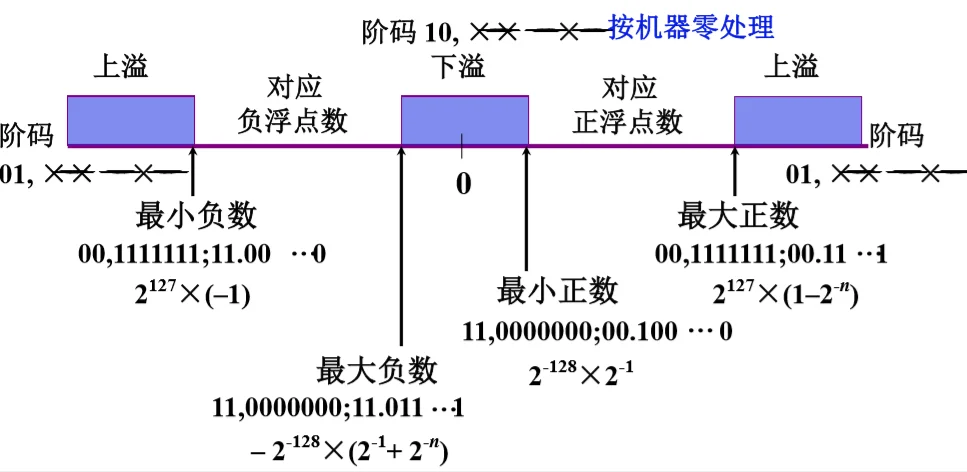
溢出判断 @
设机器数为补码,尾数为规格化形式,并假设阶符取 2 位,阶码的数值部分取 7 位,数符取 2 位,尾数取 n 位,则该补码在数轴上的表示为
算术逻辑单元 @
ALU 电路 @
组合逻辑电路,Ki不同取值, Fi不同
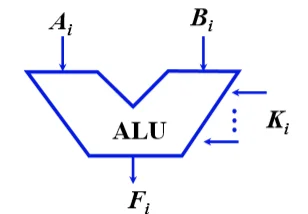
四位 ALU 74181,M=0 算术运算,M=1 逻辑运算,$S_3 - S_0$不同取值,可做不同运算。
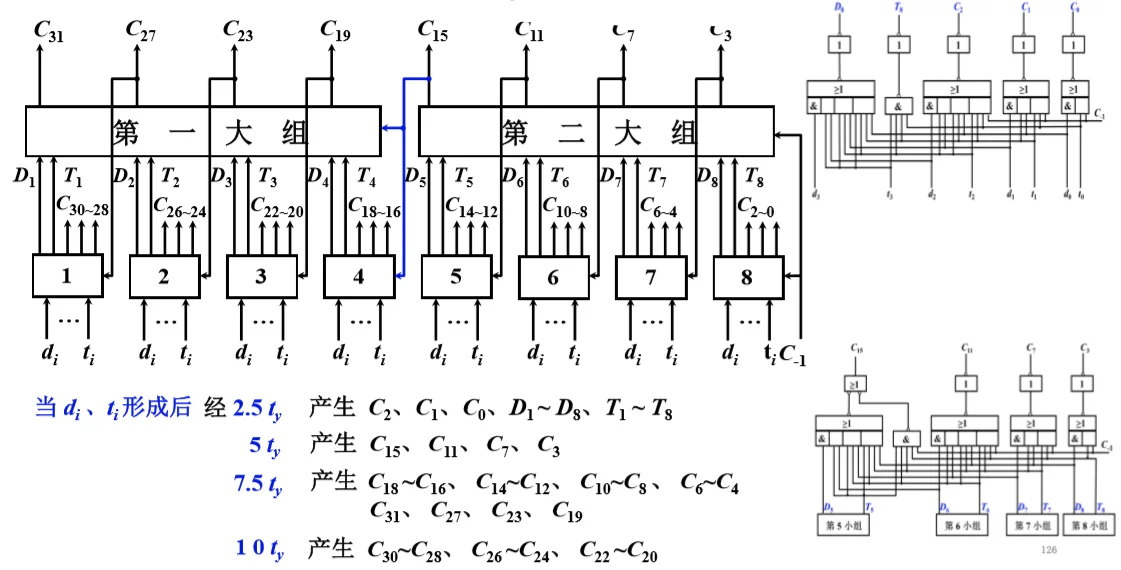
快速进位链 @
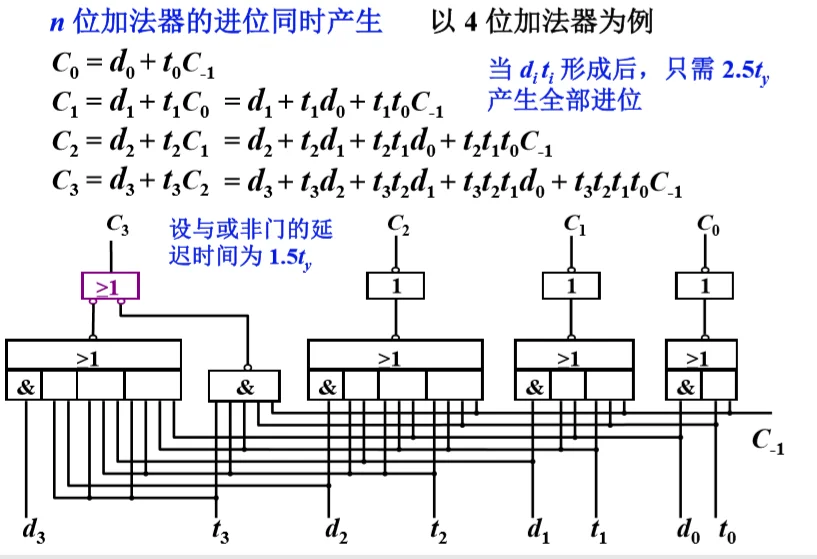
- 并行加法器
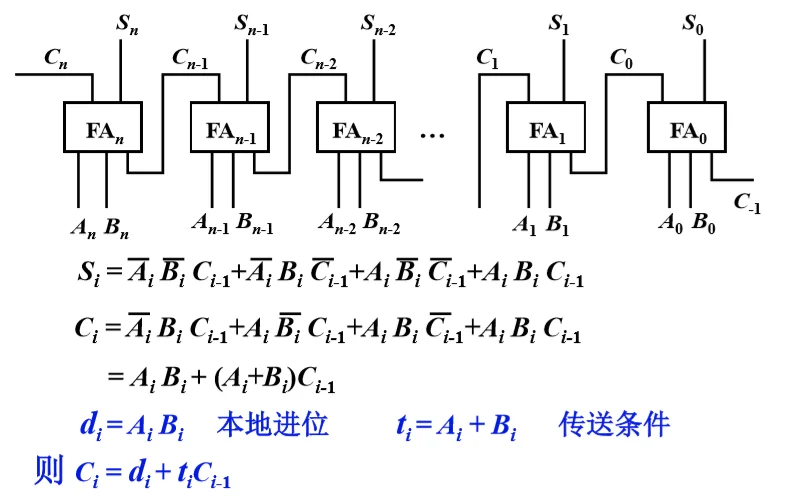
- 串行进位链
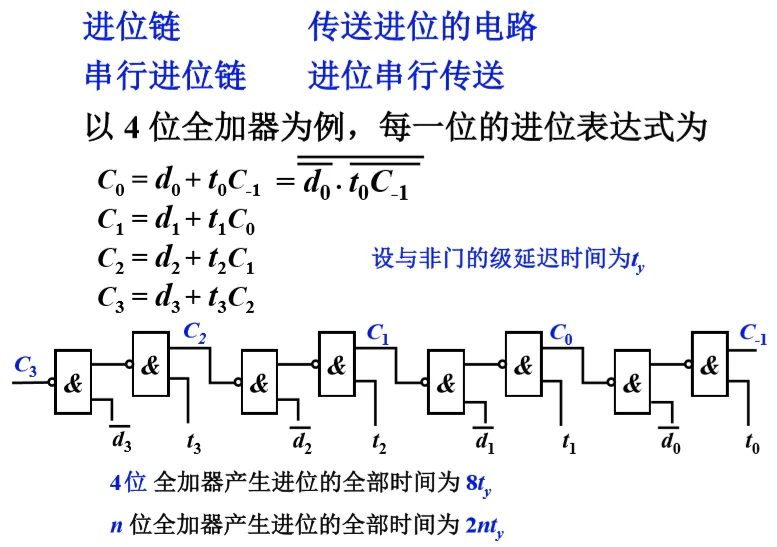
-
并行进位链(先行进位,跳跃进位)

-
单重分组跳跃进位链
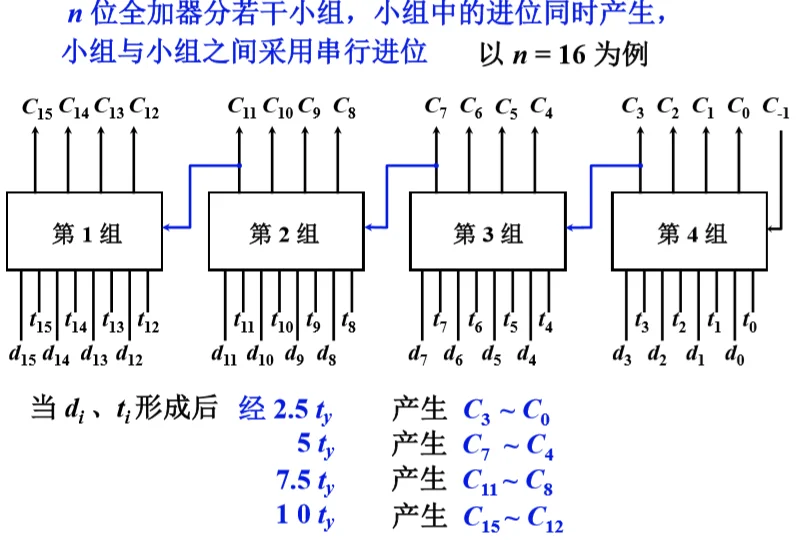
- 双重分组跳跃进位链

- 双重分组跳跃进位链,大组进位分析
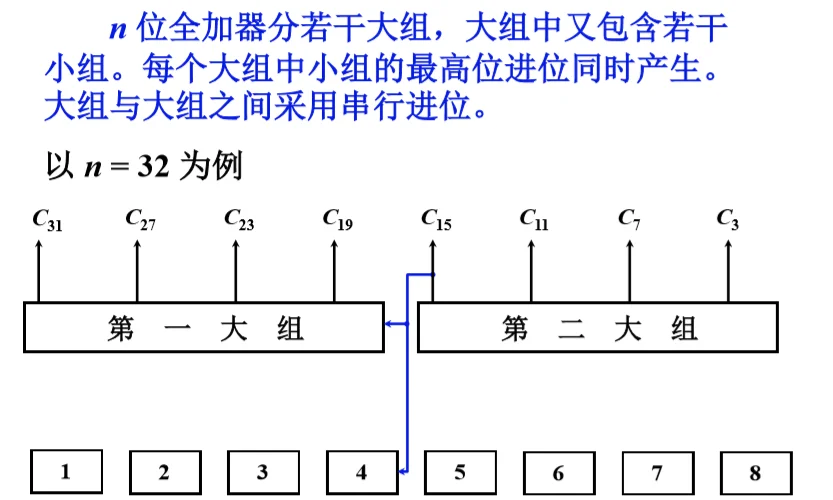
- 双重分组跳跃进位链的大组进位线路

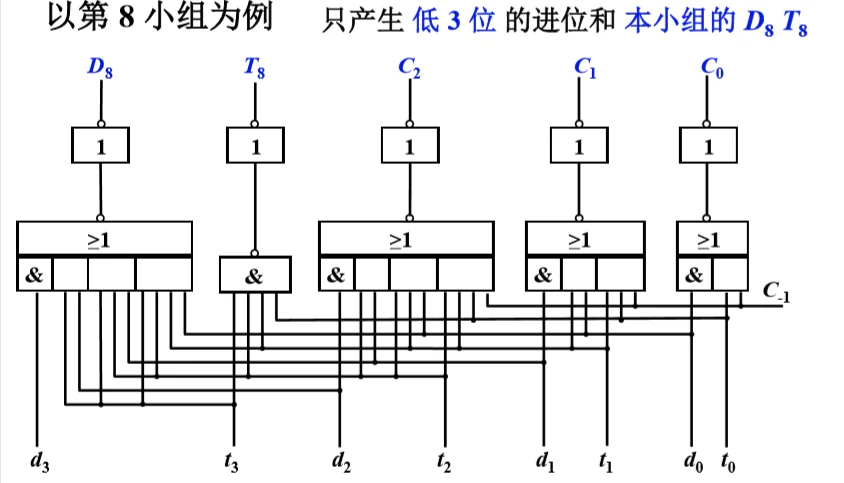
- 双重分组跳跃进位链的小组进位线路
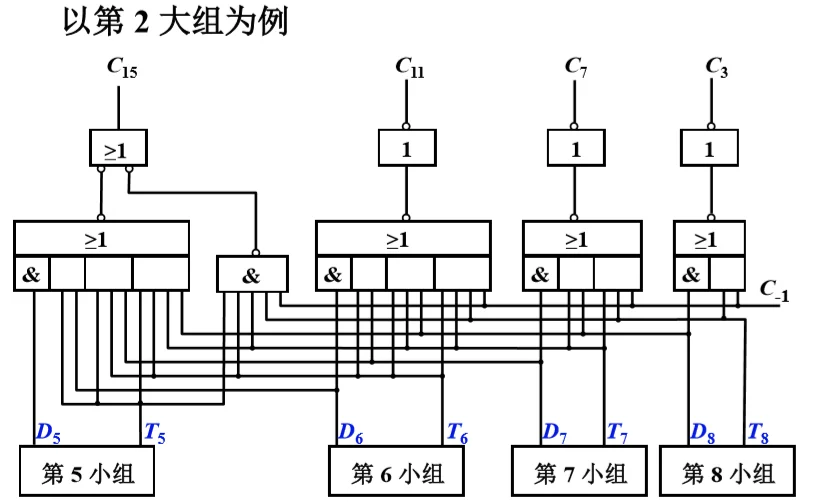
- n=16 双重分组跳跃进位链
- n=32 双重分组跳跃进位链